Blockchain - Checksums and Hashes - The roots of blockchains
Index of all Chipkin blockchain articles : Index
Download the PDF version of this article here : Download

Checksums
and Hash's
The roots of the blockchains.
Peter Chipkin
Contents
Checksums in Data Communications
Checksum or Hash – Jargon Watch
What is a hash (and checksum) – A simple example
Examples of cryptographic hash functions
Linked List with Hash Pointers – The Foundation of Block Chain.
Introduction
How do you compare two editions of the same book to see that they contain the same text.
Method 1 – word for word comparison
Method 2 – Feed both into a hashing algorithm. If the hashes are the same then the books are the same.
So what is hashing?
In simple terms, hashing means taking an input string of any length and giving out an output of a fixed length. A hashing algorithm is a mathematical function that condenses data to a fixed size.
Credit Card Numbers
Credit card numbers are often typed in, input, transferred and quoted. All of this transmission can cause errors, especially considering that humans are involved. Humans often make mistakes in transferal. To try and minimize this, credit card numbers contain a check digit.

16 Digit Credit Card numbers actually contain a 15 digit number. The last digit, the 16th, is calculated using the other 15 digits and a special formula.
The formula is specially designed to catch the common errors that are made by humans when they type their number in. Like transposing – switching 2 digits around.

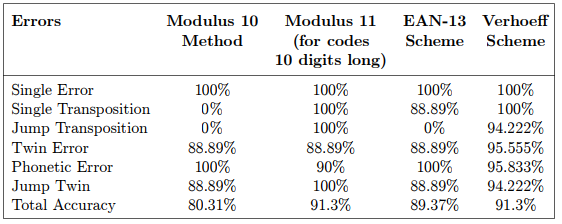
On the table below you can see the Moduslus11 checksum detects 100% of 'Single Error', 'Single Transposition' ….. In other words, Moddulus11 is truly excellent at its job
Checksums in Data Communications
We don't choose checksums, the protocols we use do. But what if were designing a protocol from scratch ?
CHIPKIN has reviewed the science for you.
Here are the main conclusions.
1. Ethernet, TCP and IP Checksums in almost all cases make the protocol checksum redundant.
2. If your data isn't random you should take care not to assume general purpose checksums are applicable.
Example – you choose to use CRC as a protocol checksum for messages relayed over TCP/IP. This could be an error because CRCs are particularly good at detecting common errors caused by noise in transmission channels. That is your least likely source of error on an ethernet packet so your choice of checksum seems inappropriate.
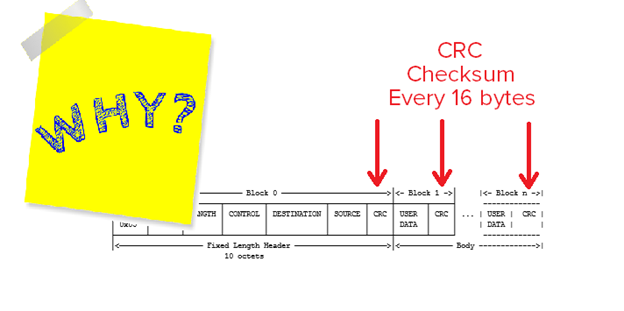
Checksums gone nuts
Consider a DNP3 (the protocol use in the power generation and distribution business) packet. The protocol designers went mad. '
Checksum or Hash – Jargon Watch
We call a hash that has been designed to detect data transmission errors and which are embedded in the data – we name these checksums.
It also depends where you live. If you live in a world of block chain nerds you will be talking about hash's. If you live in a room of embedded communications people then you will be talking about checksums. Checksums tend to be one or two bytes long. Most commonly used hash's in 2017 are 16 or 32 bytes long).
What is a hash (and checksum) – A simple example
Say each letter of the alphabet has a number assigned to it.
A=1 , B=2 etc
Then
Adam = 1,4,1,13
With Hashing Rule = sum all the letters
hash = 1 + 4 + 1 + 13 = 19
With Hashing Rule = sum all the letters and take the last digit of the sum
1 + 4 + 1 + 13 = 19 , last digit = 9 therefore hash = 9
This hashing rule make the hash fixed length.
· A "hash" (also called a "digest", and informally a "checksum") is a kind of "signature" for a stream of data that represents the contents.
· Hashes are "digests", not "encryption"
· Encryption transforms data from a cleartext to ciphertext and back (given the right keys)
· "Encryption" is a two-way operation. Hashing is not.
File Hashing
The publisher provides the file to download and the MD5 hash of the file.
You download the file. You calc the MD5 hash. You compare it to the publishers. Now you know you have the authentic file.
Used to use MD5 but now that is considered cracked.
Now often use PGP signatures.
Password Hashing
· It's a bad idea for computer systems to store passwords in cleartext (in their original form)
· A more secure way is to store a hash of the password, rather than the password itself.
· Since these hashes are not reversible, there is no way to find out for sure "what password produced this hash?" - and the so consequence of a compromise is much lower.
· Also means employees can't steal passwords
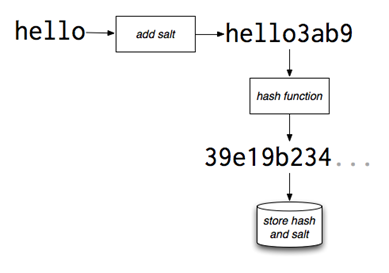
· Salt = extra string added to make it a bit harder to reverse.
MD5 Hash
Not considered safe anymore after collisions were found.
SHA256 Hash
The SHA (Secure Hash Algorithm) is one of a number of cryptographic hash functions. A cryptographic hash is like a signature for a text or a data file. SHA-256algorithm generates an almost-unique, fixed size 256-bit (32-byte) hash.
Hash is a one way function – it cannot be decrypted back.
NOTE: Tiny change in input produces a big change in the hash.
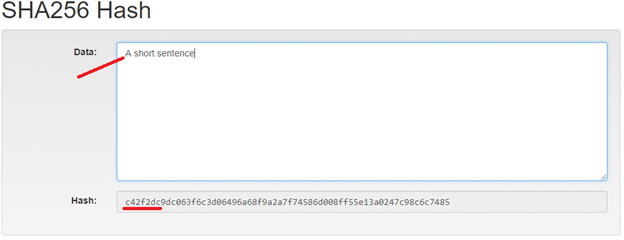
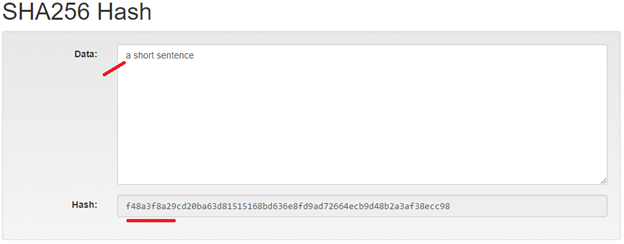
AND THEREFORE
From now on we assume that if the hash is different then the input data / text is different.
1. If the hash is the same then the data is the same
2. The assumption is not true but its statistically effective.
As you can see, in the case of SHA-256, no matter how big or small your input is, the output will always have a fixed 256-bits length. This becomes critical when you are dealing with a huge amount of data and transactions.
So basically, instead of remembering the input data which could be huge, you can just remember the hash and keep track. Before we go any further we need to first see the various properties of hashing functions and how they get implemented in the blockchain.
Attributes of a Useful Hash
Attribute #1 - Deterministic
This means that no matter how many times you parse through a particular input through a hash function you will always get the same result. This is critical because if you get different hashes every single time it will be impossible to keep track of the input.
#2 - Quick Computation
The hash function should be capable of returning the hash of an input quickly. If the process isn't fast enough then the system simply won't be efficient.
The hash function should be capable of returning the hash of an input quickly. If the process isn't fast enough then the system simply won't be efficient.
#3 - Small Changes In The Input Changes the Hash.
Even if you make a small change in your input, the changes that will be reflected in the hash will be hug
|
Input |
SHA-256 Hash |
|
Test12345 |
106ac304ae39bc4029db0faf0d1734bd5a1dc2474331e8e17039365847536d7 |
|
test12345 |
6fec2a9601d5b3581c94f2150fc07fa3d6e45808079428354b868e412b76e6bb |
#4 - Collision Resistant
Given two different inputs A and B where H(A) and H(B) are their respective hashes, it is infeasible for H(A) to be equal to H(B). What that means is that for the most part, each input will have its own unique hash
It is much easier to break collision resistance than it is to break preimage resistance. No hash function is collision free, but it usually takes so long to find a collision. So, if you are using a function like SHA-256, it is safe to assume that if H(A) = H(B) then A = B.

#5 - Puzzle Friendly
For every output "Y", if k is hugely it is infeasible to find an input x such that
H(k concatenated with x) = Y.
Hash Pointer
The pointer in a block that points to the next block has two components
1. The hash of the previous block header
AND
2. The pointer to the previous block

Examples of cryptographic hash functions
There are hundreds of hashing algorithms out there and they all have specific purposes – some are optimized for certain types of data, others are for speed, security, etc.
· MD 5: It produces a 128-bit hash. Collision resistance was broken after ~2^21 hashes.
· SHA 1: Produces a 160-bit hash. Collision resistance broke after ~2^61 hashes.
· SHA 256: Produces a 256-bit hash. This is currently being used by Bitcoin.
· Keccak-256: Produces a 256-bit hash and is currently used by Ethereum.
If you see "SHA-2," "SHA-256" or "SHA-256 bit," those names are referring to the same thing.
Linked List
Linked lists – Each object contains 2 elements – data and a pointer to the next item in the list.
Big advantage – Logical and physical order are now separate.
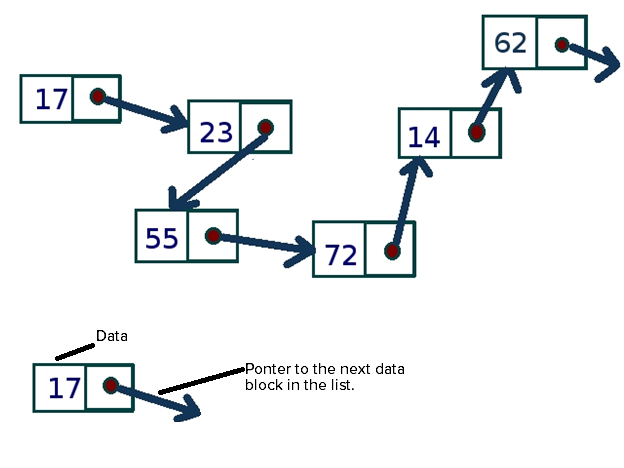
Linked List with Hash Pointers – The Foundation of Block Chain.
Data Block
HASH of this Data and append the Hash to the data.
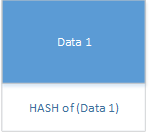
BUT This time before you calc the hash on your own data, you add the hash of the previous block to your data
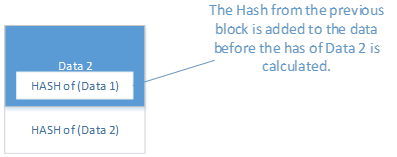
NOW Block 3 knows when block 2 is changed because it knows what block 2 hash should be and it can recalc the hash and compare them.
AND
Block 3 will also know if someone tried to change the order of the blocks or insert a new block because the hash's wont be the same.
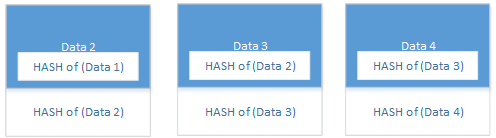
PROFOUND = Its easy to tell if anything changed. The data or the order of the blocks. If you can detect change easily then its easier to trust the data.
JARGON WATCH
Block Chain Ledger = Think of the Hashed linked list . This is the ledger.
Hashing Hashes – Building Blocks of the Blockchain ledger.
Merkle Trees
Merkle ( a person) realized its easier working with hashes of hashes than with large original blocks of data that keep growing longer. He defined the maths and methods to a specific method of hashing hashes of blocks of data.
Each block contains thousands and thousands of transactions. It will be very time inefficient to store all the data inside each block as a series. Doing so will make finding any particular transaction extremely cumbersome and time-consuming. If you use a Merkle tree, however, you will greatly cut down the time required to find out whether a particular transaction belongs in that block or not.
These notes assume that new data/changes are appended rather than edited in place in old data blocks which have already been hashed.
We want to add some data to a file. ( Add file 2 to File 2)



Using a hash tree like a Merkle tree:
1. Significantly reduces the amount of data that a trusted authority has to maintain to proof the integrity of the data.
2. Significantly reduces the network I/O packet size to perform consistency and data verification as well as data synchronization.
3. Separates the validation of the data from the data itself -- the Merkle tree can reside locally, or on a trusted authority, or can itself reside on a distributed system (perhaps you only maintain your own tree.) Decoupling the "I can prove the data is valid" from the data itself means you can implement the appropriate and separate (including redundant) persistence for both the Merkle tree and the data store.
So the answer to the why is three-fold:
1. Merkle trees provide a means of proving that integrity / validity of your data.
2. Merkle trees require little memory / disk space and proofs are computationally easy and fast.
3. Merkle tree proofs and management requires only a very small and terse amount of information to be transmitted across a network.
Merkle trees (and variations) are used to provide:
· consistency verification
· data verification
· data synchronization
Consistency Verification
Merkel or Hash trees allow for easy consistency validation.
Instead of comparing the data, you compare the tree of hashes. This is fast and easy. It does NOT prove the data is the same but it proves the hash trees are consistent.
A "consistency proof" lets you verify that any two versions of a Hash Tree are consistent:
1. the later version includes everything in the earlier version
2.
...in the same order
3. ...and all new records come after the records in the older version
"If you can prove that a Hash Tree is consistent it means that:
· no certificates [records] have been back-dated and inserted into the Hash Tree
· no certificates have been modified in the Hash Tree,
· and the Hash Tree has never been branched or forked.
It is time consuming and computationally expensive to check the entirety of each file whenever a system wants to verify data. So, this why Merkle trees are used. Basically, we want to limit the amount of data being sent over a network (like the Internet) as much as possible. So, instead of sending an entire file over the network, we just send a hash of the file to see if it matches. The protocol goes like this:
1. Computer A sends a hash of the file to computer B.
2. Computer B checks that hash against the root of the Merkle tree.
3. If there is no difference, we're done! Otherwise, go to step 4.
4. If there is a difference in a single hash, computer B will request the roots of the two subtrees of that hash.
5. Computer A creates the necessary hashes and sends them back to computer B.
6. Repeat steps 4 and 5 until you've found the data blocks(s) that are inconsistent. It's possible to find more than one data block that is wrong because there might be more than one error in the data.
Data Synchronizaton
Merkle trees are useful in synchronizing data across a distributed data store because it allows each node in the distributed system to quickly and efficiently identify records that have changed without having to send all the data to make the comparison.
Making A Merkle Tree
They are binary.
Take any 2 records and calculate the hash of each.
Allocate a parant node to the two records (leaves)
In that node store the hash of the two child hashes.
Repeat until every 2 records (it's a binary process) has a parant
Repeat until each 2xparants have a parant
Repeat until you have reached the top of the pyramid. This is called the Root Node.
Merkle Tree More Reading
https://brilliant.org/wiki/merkle-tree/
Index of all Chipkin blockchain articles : Index
Download the PDF version of this article here : Download

