How Tax Cheats Are Caught – Random Numbers Are Less Random Than You Think
Locating Tax Cheats with Benford's Law
People who make up numbers on their tax returns are easily caught. Because, for all the numbers on a tax return - 30% begin with a '1' and 17% with a '2' and .... only 5% with a '9'. If you make up numbers and they don't fall into this frequency distribution, then they know you are trying to cheat the system. Thanks to Benford's Law, the IRS and CRA know this and use it.
Did you know that 30% of all goods sold in the world have a price that begins with a '1', while only 5 percent start with the number '9'? This is true for city populations, river length, the number of hairs on a person's head. .... almost every set of random numbers. Its true - year after year after year, it's crazy!
What is a Benford's Law?
Benford's Law - The first numerals of numbers found in series of records (of the most varied sources) do not display a uniform distribution, but rather are arranged in such a way that the digit "1" is the most frequent, followed by "2", "3", and so in a successively decreasing manner down to "9".
Below is an illustration:
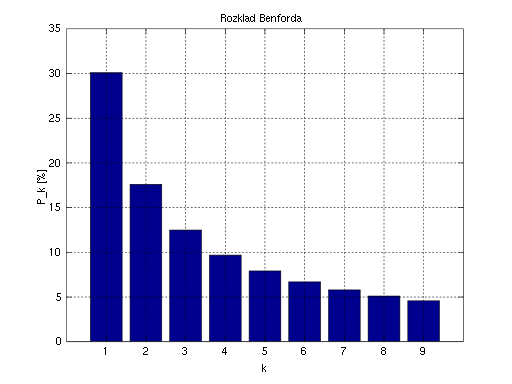
Example
A cutoff of $2,500 USD for purchases in which a purchase order is required for any purchase at or above this price point. Thus, a Benford's Law test of the two leading digits (specifically, 24) could reveal any anomalies, manipulation or fraud involving this cutoff. The law is also used as a test of controls to see if existing controls for purchase orders are working effectively. Note Since the cutoff amount has two key digits, a two-digit test is needed rather than a single leading digit.
Other Applications Include Analysis of:
- Credit card transactions
- Purchase orders
- Loan data
- Customer balances
- Journal entries
- Stock prices
- Accounts payable transactions
- Inventory prices
Examples of data sets that are not likely to be suitable for Benford's Law include:
- Airline passenger counts per plane
- Telephone numbers
- Data sets with 500 or fewer transactions
- Data generated by formulas (e.g., YYMM#### as an insurance policy number)
- Data restricted by a maximum or minimum number (e.g., hourly wage rate)
- The two-digit tests usually give more granular results, but are also likely to reveal more spikes than a one-digit test.
The spikes above the Benford's Law line are the numbers of interest. Independent information is then obtained from the spikes.
Constraints in Using Benford's Law
The assumptions regarding the data to be examined by Benford's Law are:
- Numeric data
- Randomly generated numbers
- Not restricted by maximums or minimums
- Not assigned numbers
- Large sets of data
- Magnitude of orders (e.g., numbers migrate up through 10, 100, 1,000, 10,000, etc.) (Other assumptions exist that are unimportant in applying Benford's Law in IT audits).
- The mathematical theory has always been applied to digital analysis, i.e., a logarithmic study of the occurrence of digits by position in a number.
In Benford's Law numbers in a large data set are randomly generated. For example, hourly wages will have a minimum and possibly some maximum (even if a realistic maximum) that means that the data set is not generated in a completely random fashion, but rather uses a restricted set of digits as the potential leading digit.
The same is true if there is a formula to the way the number is generated. For example, US telephone numbers are assigned with a specific area code and a limited number of 3-digit prefaces to the last 4 digits (which are the only truly randomly generated numbers in a phone number). Thus, before applying Benford's Law, ensure that the numbers are randomly generated without any real or artificial restriction of occurrence.
Benford's Law should be applied only to large data sets such as files with hundreds of transactions (e.g., invoices to customers, disbursements, payments received, inventory items. Using less data can lead to too many spikes of interest.
Conclusion
Benford's Law can recognize the probabilities of highly likely or unlikely frequencies of numbers in a data set. The probabilities are based on mathematical logarithms of the occurrence of digits in randomly generated numbers in large data sets. Benford's Law can be used in tests of controls and other tests of data sets. However, the constraints should be compatible with the data set to be tested.
References
- Image Credit: Wikipedia, https://en.wikipedia.org/wiki/Benford%27s_law#/media/File:Rozklad_benforda.svg
- https://www.isaca.org/resources/isaca-journal/past-issues/2011/understanding-and-applying-benfords-law
- https://brilliant.org/wiki/benfords-law/
- https://www.journalofaccountancy.com/issues/2017/apr/excel-and-benfords-law-to-detect-fraud.html
- https://en.wikipedia.org/wiki/Benford%27s_law#Krieger-Kafri_entropy_explanation


